版權聲明:本文為博主原創文章,遵循 CC 4.0 BY-SA 版權協議,轉載請附上原文出處鏈接和本聲明➜。
本文鏈接👂:https://blog.csdn.net/tianxiawushanu/article/details/142660275
1. 排序的概念及其應用
在正式講解插入排序和希爾排序之前,我要帶著大家理解我們為什麽需要排序?以及排序在我們生活中有什麽應用?學完這些之後,大家也許對排序算法就不會那麽迷茫了⚓️。
1.1 排序的概念
排序🌬🧚🏿♂️:所謂排序↗️,就是使一串記錄👩🏼⚕️,按照我們特定且可行的想法,遞增或遞減的排列起來的操作🪔。
排序是一項操作!
1.2 排序的應用
看到這裏⏪,大家可以打開京東商城🙂↔️,當你想買一臺新的手機時🧑🧒🧒,卻不知如何入手🤦🏼♂️。你可能會選擇按好評數來進行排序🍬,從而選出好評率最高的手機。在這個過程,就用到了排序的思想。
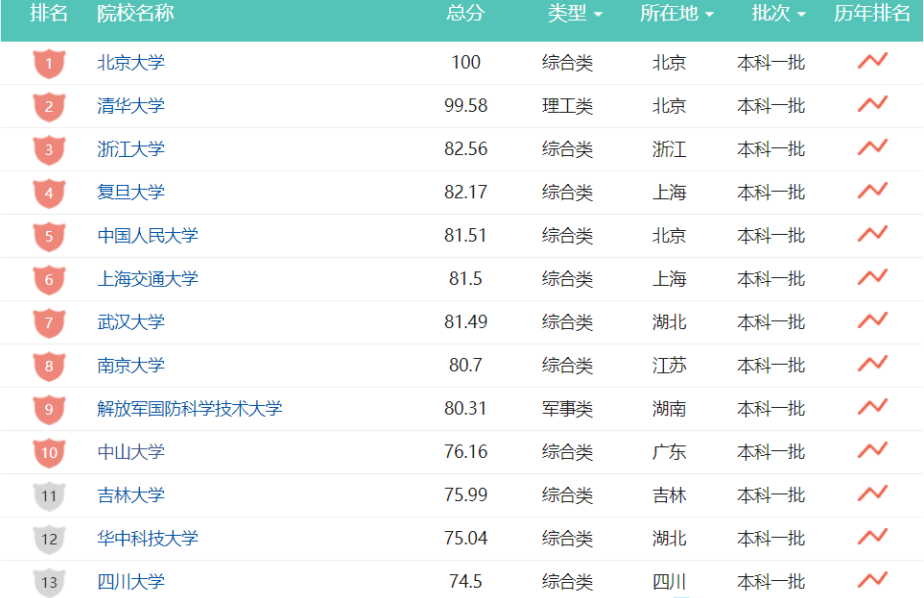
再如,我們的大學按照教學資源以及教學能力🧜🏻♂️,也能進行排序😟:
當然,生活中還有很多例子都是用到了排序的思想。這就是所謂處處有排序!
好了🧑🧑🧒,在了解完排序的重要性之後,我們就要正式邁入學習插入排序和希兒排序的殿堂中了。

2. 插入排序
插入排序🥮,通常我們也稱它為直接插入排序。
2.1 基本思想
在一個有序的數組中🫴🏿,按照一定的規則插入待排序的數字🥦。
詳細一點說的話☔️,就是🏺🐤:
算法思路:
先從單趟排序講起,我們可以選擇待插入的數字與從排序好的數組末端的數進行比較。若發現該值比待插入的數字要大,則將蓋子往後挪動一位,接著繼續往前面進行比較。若發現該值比待插入的數字要小,說明該值的後面一個位置就是待插入數字應該插入的位置🧑🏽🦰,我們就可以結束循環了。
單趟排序講完了之後📁,就可以將一個完整的插入排序了🤟🏼。
如果你真的認證解讀了單趟插入排序的思路,你會發現插入排序不過如此🕘!
其實一個完成的插入排序就是在循環地跑單趟排序,循環地初始條件為從待插入數組的第二個元素小標開始🙅🏽。每當單趟排序跑完之後🏓,我們都得設置循環條件的值(一開始比較數組末端的位置)。因為你已經排好了部分數組,每當來一個新數字就得在拍好數組中插入,重復上述過程。
下面我給大家展示插入排序算法的動圖,希望大家能夠結合上述的話語👨🏽🏭,仔細觀看:
2.2 插入排序的代碼實現
void InsertSort(int* a, int n){
for (int i = 1; i < n; i++)
{
int end = i - 1; //待排序數組的末端
//也可以寫成int tmp = a[end + 1];
int tmp = a[i]; //tmp存放的是待插入的數值
while (end >= 0)
{
if (tmp < a[end]) //待插入數字與數組末端的值進行比較
{
a[end + 1] = a[end];
end--;
}
else
{
break;
}
}
a[end + 1] = tmp;
}
}
2.3 插入排序算法總結
根據上面的代碼,我們可以總結出一些關於插入排序算法的特征:
元素集合越接近有序,直接插入排序算法的時間效率就越高
- 時間復雜度:O(N^2)
- 空間復雜度:O(1)
,它是一種穩定的排序算法
穩定性:穩定
3. 希爾排序
希爾排序又稱縮小增量排序。
3.1 基本思想
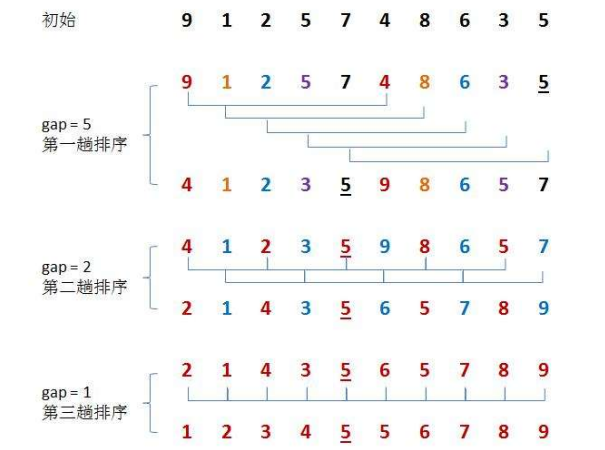
先選定一個整數(gap),把待排序的數據分成個別組。分組的標準就是所有距離為gap的數據分在同一組🥳,並對每一組內的記錄進行排序。然後🙇🏼♀️,縮小gap的值👲🏼,重復上述分組和排序的工作👩🏽🎤。當gap = 1時,就相當於直接插入排序了。
上面這個思想很重要,是理解希爾排序的核心!
給大家舉個例子👨🏼🏫:
3.2 希爾排序的代碼實現
void ShellSort(int* a, int n){
int gap = n;
while (gap > 1)
{
//gap /= 2;
gap = gap / 3 + 1;
for (int j = 0; j < gap; j++)
{
//就是在對每組(隔gap位置的數字)的數據進行插入排序
for (int i = j; i < n; i += gap)
{
int end = i - 1;
int tmp = a[i];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + 1] = a[end];
end--;
}
else
{
break;
}
}
a[end + 1] = tmp;
}
}
}
3.3 希爾排序的特征總結
- 希爾排序是對直接插入排序的優化👨🚒。
當gap > 1時都是預排序👩🎨,目的是讓數組更接近於有序。當gap == 1時👵🏼🧑🏽🦲,數組已經接近有序的了,這樣就會很快🙎。這樣整體而言,可以達到優化的效果。我們實現後可以進行性能測試的對比。
希爾排序的時間復雜度不好計算↩️,因為gap的取值方法很多,導致很難去計算🛷。但是我們一般認為希爾排序算法的時間復雜度為O(N*logN),但是如果我們追求嚴謹,那它的時間復雜度為O(N^1.3)。