版權聲明：本文為博主原創文章，遵循 CC 4.0 BY-SA 版權協議，轉載請附上原文出處鏈接和本聲明。

前言

講到排序相信大家一定對一種排序很熟悉，它的名字就叫做冒泡排序。這個排序大家在學習各種語言時，都是一道繞不去的坎👩🏿‍🍳👸🏻。本文還會介紹另一個比較簡單的排序 —— 選擇排序，以及給大家講一下選擇排序的另一種寫法（但是效率沒有發生大的改變）🧎🏻‍➡️。

本章內容比較簡單，主要是講一下算法的思想，以及給大家總結一下我們在寫排序算法時的一些小技巧🟧。

1. 冒泡排序

在講冒泡排序的算法之前，先給大家看一個動圖，大家可以結合動圖的演示理解我下面所講的話語🚣。

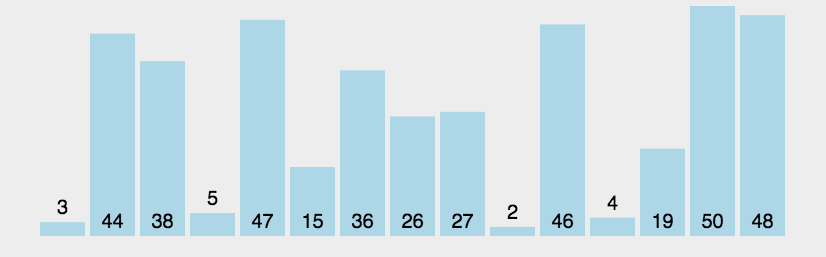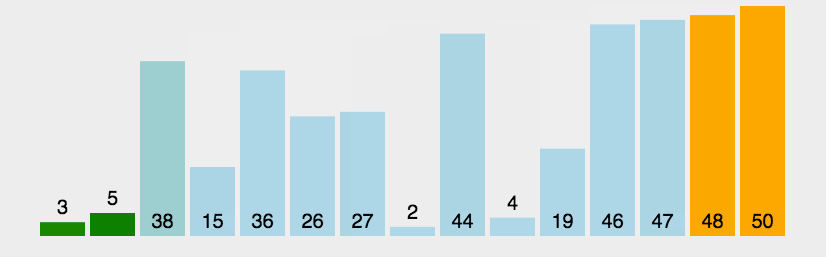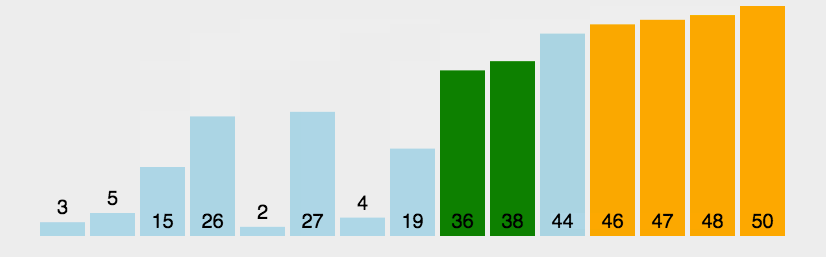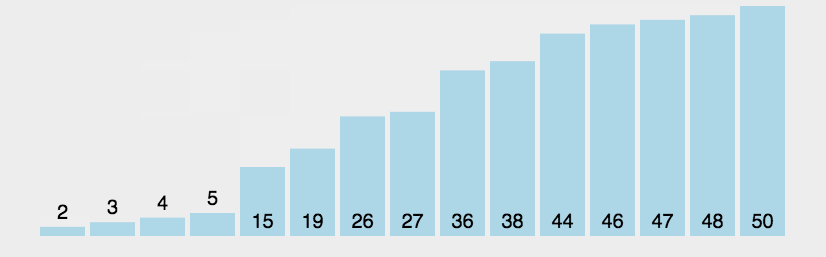
1.1 算法思想

這裏我們先理解冒泡排序算法的單趟排序思想💴。這裏我們主要講的是升序排序（降序一樣的道理 ）。

🍉結合上面的動圖，我們可以很清楚的看到，冒泡排序的核心思想就是將數組中相鄰的兩個數進行比較🍀，如果左邊的數比右邊的數要大⏰，那它們兩個就交換數據，接著繼續比較下一組相鄰的數據🧕🏿，如果右邊的數大於左邊的數，那就直接進入比較下一組相鄰的數據的環節。一直比較到一組相鄰數據中包含了數組末尾的數據，才算是結束。

以上就是冒泡排序單趟排序的思想！

接著我們就得組合多次單趟排序形成一個完整的冒泡排序⚆。

🍉我們可以這麽想🦻🏿：冒泡排序單趟排序的目的是為了將待排序數組中的最大值給放到待排序數組的結尾處，緊接著就縮小待排序的區間範圍。又得讀者可能會問為什麽要縮小待排序的區間範圍🙎🏽‍♀️？原因很簡單，因為單趟排序的最大數引進放到了正確的位置上了♥︎，下一次排序可以不用動它了🕸。這樣一來，只要一開始數組有n個元素，我們執行單趟排序的次數就為(n-1)次🤾🏿‍♀️。

好了🔸，思想講解完了🍼💋，下面直接上代碼🙇。

1.2 冒泡排序的代碼實現

//交換兩個數字void Swap(int* p1, int* p2){
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;}//冒泡排序 -- 第一種寫法void BubbleSort(int* a, int n){
	for (int i = 0; i < n; i++)
	{
		for (int j = 1; j < n - i; j++)
		{
			if (a[j - 1] > a[j])
			{
				Swap(&a[j - 1], &a[j]);
			}
		}
	}
	}

//冒泡排序 -- 第二種寫法//交換兩個數字void Swap(int* p1, int* p2){
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;}void BubbleSort(int* a, int n){
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n - i - 1; j++)
		{
			if (a[j] > a[j + 1])
			{
				Swap(&a[j + 1], &a[j]);
			}
		}	
	}
	}

排序算法的改進

大家如果仔細的一點的話可以發現一個問題💚，如果我給的數組是一個已經有序的數組🙏🏼🤹‍♂️，它仍會給我進行一次完整的冒泡排序🧓🏿，可以通過以下代碼給大家測試一下⚒：

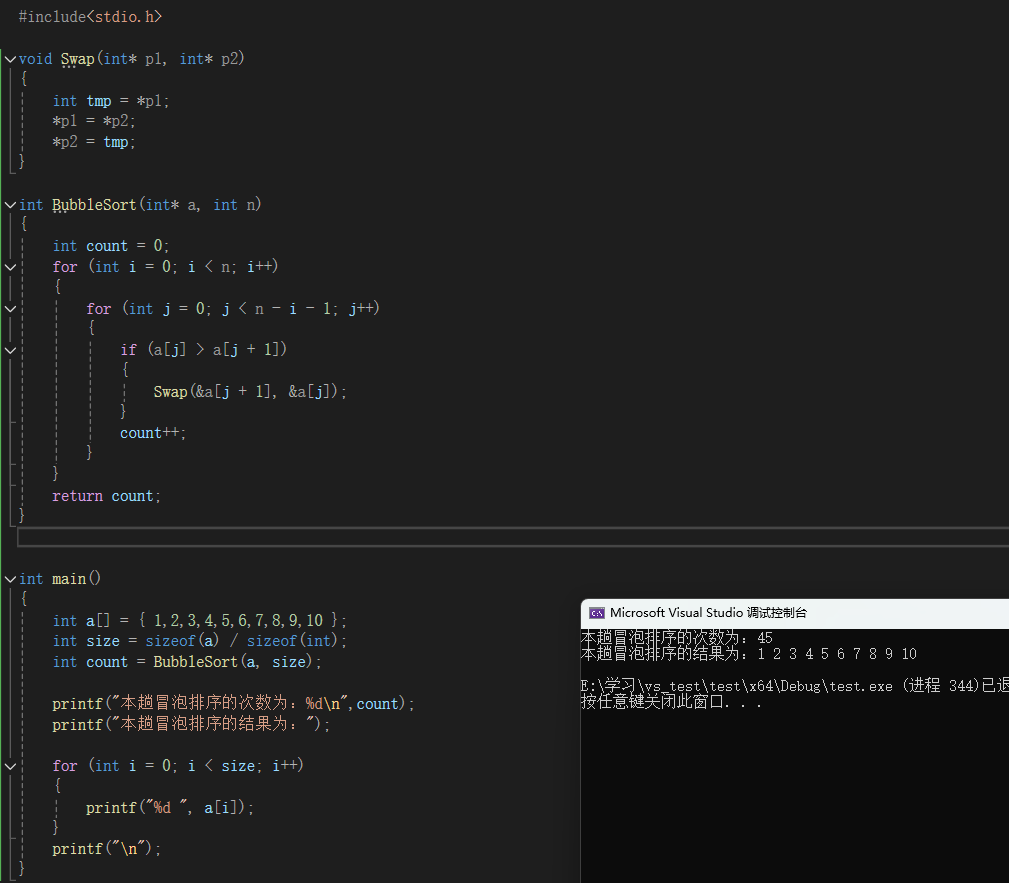
可以看到無論我們餵給這個函數什麽數組，這個排序的時間復雜度都為O(N^2)。但是這跟我們的預期是不一樣的，因為冒泡排序在排有序數組的時間復雜度應該為O(N)🙋🏿‍♂️。所以我們該怎麽對上面的代碼進行優化呢？

優化之後的代碼：

//冒泡排序 -- 第二種寫法//交換兩個數字void Swap(int* p1, int* p2){
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;}void BubbleSort(int* a, int n){
	for (int i = 0; i < n; i++)
	{
		int flag = 0; //設定一個標誌位🈷️，又來標明該數組是否有序
		
		for (int j = 1; j < n - i; j++)
		{
			if (a[j - 1] > a[j])
			{
			    flag = 1; //說明數組時無序的
				Swap(&a[j - 1], &a[j]);
			}
		}
		
		if(flag == 0)
		{
			break;
		}
	}
	}

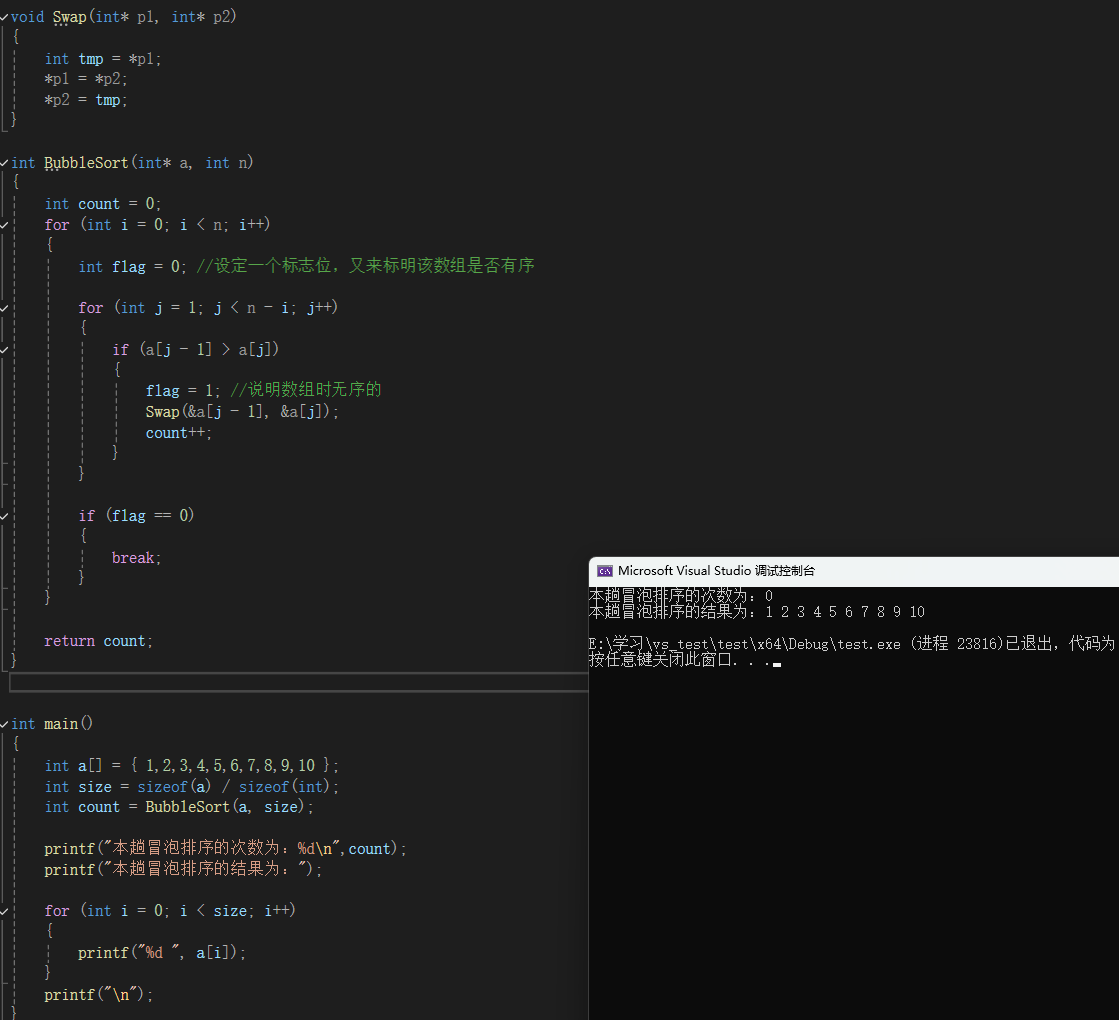
可以很清楚的看到，我們的改良大獲成功。

2. 選擇排序

老規矩（以升序為例），先上動圖🧑🏽‍🍼：

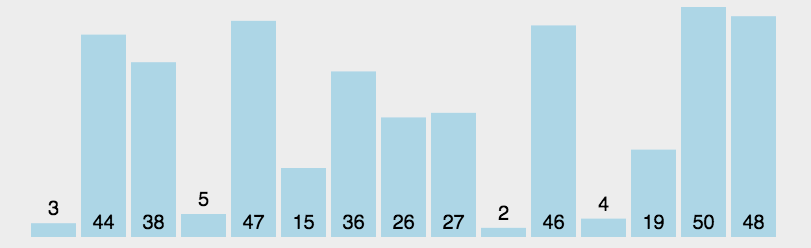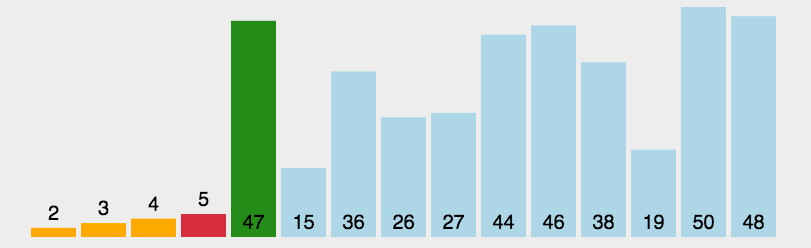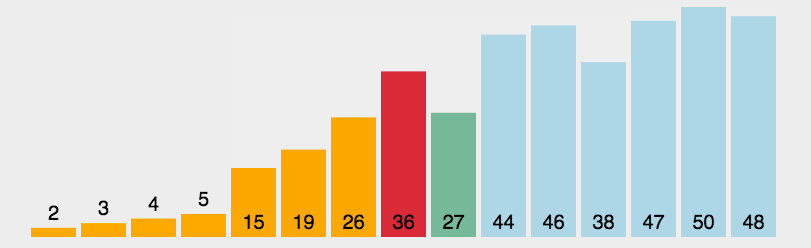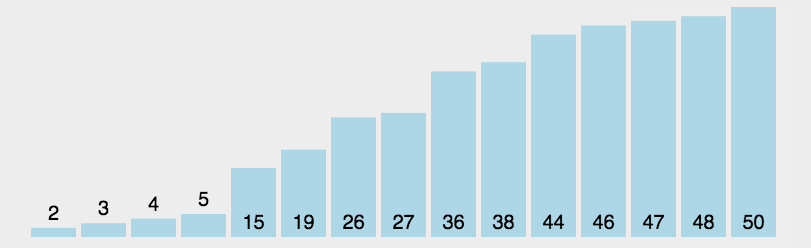
2.1 算法思想

選擇排序的單趟排序是選擇待排序數組中最小的數🏄🏽，將它與待排序數組中的開頭的位置的數交換位置💂🏼。這樣單趟排序就完成了🧙🏻。

接下來講一下完整的選擇排序🐪，可以看到的是每當我們完成了一個選擇排序算法的單趟排序是將待排序的數組中最小的數放到正確的位置上🧚🏿。直到最後只剩最後一個數字時，排序終止。

2.2 選擇排序的代碼實現

選擇排序算法的第一種寫法：

void SelectSort(int* a, int n){
	for (int i = 0; i < n; i++)
	{
		int mini = a[i];
		for (int j = i; j < n; j++)
		{
			if (a[mini] > a[j])
			{
				mini = j;
			}
		}
		Swap(&a[mini],&a[i]);
	}
	}

選擇排序算法的第二種寫法🎞：

void SelectSort(int* a, int n){
	int left = 0, right = n - 1;
	int maxi = 0, mini = 0;


	while (left < right)
	{
		for (int i = left; i <= right; i++)
		{
			if (a[maxi] < a[i])
			{
				maxi = i;
			}

			if (a[mini] > a[i])
			{
				mini = i;
			}

		}

		Swap(&a[left], &a[mini]);

		if (left == maxi)
		{
			maxi = mini;
		}
		Swap(&a[right], &a[maxi]);

		left++;
		right--;
	}
	}

上面的寫法比較難以理解，如果實在理解不了的話🙅🏿，第一種寫法也是可以的🐎。因為這兩種寫法的效率是差不多的，時間復雜度都為O(N^2)。

3. 寫排序算法的小技巧

🍉相信大家在看完每個排序算法的思路講解時，會發現一個規律：從單趟排序開始分析，在逐步向全局排序進行延伸➙。核心就在於我們得理解單趟排序的目的是什麽，這樣才能為我們的全局排序做鋪墊🤷🏻。